Зависимость скорости химических реакций от температуры установил

Зависимость скорости химических реакций от температуры установил Вант-Гофф в 1880 году и сформулировал эмпирическое правило Вант-Гоффа:

Скорость большинства реакций увеличивается в 2-4 раза при повышении температуры на 10 градусов,если реакция проводится при  температуре,близкой к комнатной.

Например,время,необходимое для уменьшения концентрации реагента вдвое газообразного оксида азота Ⅴ при 35гр.C составляет около 85 мин,при 45°С-около 22 мин,при 55°C-около 8 мин.

Можно объяснить это следующим образом на примере гомогенной реакции в газовой фазе.Для протекания реакции необходимы столкновения молекул.При этом какие-то химические связи рвутся,другие образуются.Получаюся другие молекулы,молекулы продукта реакции.Значит,скорость реакции зависит от числа столкновений.Но так как средняя скорость молекул пропорциональна квадратному корню из абсолютной температуры,т.е. при повышении температуры на 10 градусов,например,от 300 до 310 К,средняя скорость молекул возрастёт лишь в 1.02 раза,т.е. гораздо меньше,чем требует правило Вант-Гоффа.

Значит,кроме увеличения числа столкновений действует ещё какой-то важный фактор.Чтобы найти его,необходимо провести более подробный анализ поведения большого числа частиц при различных температурах.

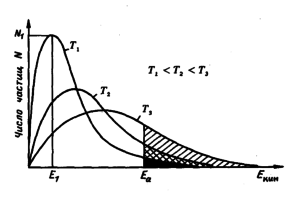
Рис. 2

По законам статистики отдельные частицы могут иметь скорость и энергию отличную от средних значений.Это показано на рис.2,где видно распределение частиц по кинетической энергии в зависимости от температуры.

Рассмотрим кривую для температуры Т1.Общее число частиц в системе пропорционально площади под кривой.Кинетической энергией E1 для данной температуры обладает число частиц,равное N1.Частицы с большей энергией расположены справа от E1,а с меньшей-слева.

Рассмотрим энергию Ea,большую чем E1.При температуре T1 число частиц с энергией большей Ea составляет меньшую часть от общего числа частиц,что соответствует зачерненной площади под кривой T1.При более высокой температуре Т2 уже больше частиц обладает энергией,большей Еа,а при повышении температуры до Т3 энергия Еа оказывается близкой к средней.Доля частиц с кинетической энергией больше или равной Еа описывается уравнением

N/N0=e⁻Ea/RT

В 1889 году Аррениус вывел уравнение константы скорости реакции,которая связана с абсолютной температурой.

(А и Е — постоянные для данной реакции величины).Присутствие экспоненциального множителя в уравнении Аррениуса показывает,что скорость реакции определяется не общим числом столкновений молекул в единицу времени,а числом эффективных столкновений,для молекул с энергией не меньшей Еа,называемой энергией активации реакции.

Скорость реакции пропорциональна вероятности «удачного»столкновения-отсюда и появился в уравнении Аррениуса множитель А,или так называемый частотный фактор,имеющий размерность константы скорости и равный числу столкновений в единицу времени,умноженному на вероятность благоприятного столкновения,т.е. числу «удачных» столкновений в единицу времени.В этом и заключается важный фактор,о котором говорилось выше.